If you’re trading with options (or about to start), you will need to get acquainted with the Greeks. The Greeks are composed of four main measures of risk which represent several variables that influence option prices. They are used to support a trader or portfolio manager to determine the risk and reward in options trading.
The Greeks risk measures indicate how exposed a given option is to time value decay, implied volatility and changes in the price of the underlying instrument. Essentially, traders monitor five Greeks: Delta, Gamma, Vega, Theta, Rho (a good mnemonics to keep in mind is DGVTR).
The simple definition for each of these measures is summarised by Investopedia as follows:
Delta
Delta for individual options, and position Delta for strategies involving combinations of positions, are measures of risk from a move of the underlying price. For example, if you buy an at-the-money call or put, it will have a Delta of approximately 0.5, meaning that if the underlying stock price moves 1 point, the option price will change by 0.5 points (all other things remaining the same). If the price moves up, the call will increase by 0.5 points and the put will decrease by 0.5 points. While a 0.5 Delta is for options at-the-money, the range of Delta values will run from 0 to 1.0 (1.0 being a long stock equivalent position) and from -1.0 to 0 for puts (with -1.0 being an equivalent short stock position).
Vega
When any position is taken in options, not only is there risk from changes in the underlying but there is risk from changes in implied volatility. Vega is the measure of that risk. When the underlying changes, or even if it does not in some cases, implied volatility levels may change. Whether large or small, any change in the levels of implied volatility will have an impact on unrealized profit/loss in a strategy. Some strategies are long volatility and others are short volatility, while some can be constructed to be neutral volatility. For example, a put that is purchased is long volatility, which means the value increases when volatility increases and falls when volatility drops (assuming the underlying price remains the same). Conversely, a put that is sold (naked) is short volatility (the position loses value if the volatility increases). When a strategy is long volatility, it has a positive position Vega value and when short volatility, its position Vega is negative. When the volatility risk has been neutralized, position Vega will be neither positive nor negative.
Theta
Theta is a measure of the rate of time premium decay and it is always negative (leaving position Theta aside for now). Anybody who has purchased an option knows what Theta is, since it is one of the most difficult hurdles to surmount for buyers. As soon as you own an option (a wasting asset), the clock starts ticking, and with each tick the amount of time value remaining on the option decreases, other things remaining the same. Owners of these wasting assets take the position because they believe the underlying stock or futures will make a move quick enough to put a profit on the option position before the clock has ticked too long. In other words, Delta beats Theta and the trade can be closed profitably. When Theta beats Delta, the seller of the option would show gains. This tug of war between Delta and Theta characterises the experience of many traders, whether long (purchasers) or short (sellers) of options.
Gamma
Delta measures the change in price of an option resulting from the change in the underlying price. However, Delta is not a constant. When the underlying moves so does the Delta value on any option. This rate of change of Delta resulting from movement of the underlying is known as Gamma. And Gamma is largest for options that are at-the-money, while smallest for those options that are deepest in- and out-of-the-money. Gammas that get too big are risky for traders, but they also hold potential for large-size gains. Gammas can get very large as expiration nears, particularly on the last trading day for near-the-money options.
Rho
Rho is a risk measure related to changes in interest rates. Since the interest rate risk is generally of a trivial nature for most strategists (the risk free interest rate does not make large enough changes in the time frame of most options strategies), it will not be dealt with at length in this tutorial.
When interest rates rise, call prices will rise and put prices will fall. Just the reverse occurs when interest rates fall. Rho is a risk measure that tells strategists by how much call and put prices change as a result of the rise or fall in interest rates. The Rho values for in-the-money options will be largest due to arbitrage activity with such options. Arbitragers are willing to pay more for call options and less for put options when interest rates rise because of the interest earnings potential on short sales made to hedge long calls and opportunity costs of not earning that interest.
Positive for calls and negative for puts, the Rho values will be larger for long-dated options and negligible for short-dated ones. Strategists who use long-term equity anticipation securities (LEAPS) should take into account Rho since over longer time frames the interest rate share of an option’s value is more significant.
Position Greeks If Positive Value (+) If Negative Value (-) Delta Long the Underlying Short the Underlying Vega Long Volatility (Gains if IV Rises) Short Volatility (Gains if IV Falls) Theta Gains From Time Value Decay Loses From Time Value Decay Gamma Net Long Puts/Calls Net Short Puts/Calls Rho Calls Increase in Value W/ Interest Rates Rise Put Decrease in Value W/ Interest Rate Rise Source: http://www.investopedia.com/university/option-greeks/greeks1.asp#ixzz4K3UW9TXi
Attempting to predict what will happen to the price of an option as the market changes is an uncertain task. The main factor is that the option price doesn’t often move in correlation with the price of the underlying security. It is therefore crucial for the trader or investor to try to determine which factors affect the oscillation of an option price. The interpretation and analysis of the Greeks is essential to sustain a decision. The Greeks provide a way to measure the sensitivity of an option’s price to quantifiable factors.
An important aspect to note is that the Greeks’ values are based on theoretical, calculated figures which are based in predefined mathematical models. This means that the quality of the results for each Greek measure is as good as the quality of the mathematical model being used to calculate these figures.
The Options Monitor (OMON) bloomberg command allows us to view Options available for trading for a given instrument. In the examples below you can see the different Calls and Puts for MSFT US (different expiry dates) which is trading at $56,21. By going into the detail of a given Option e.g. MSFT US 09/16/16 C55.5 you can then look at the details for that option, namely the Greeks displayed in the volatility analysis (GIV) section. The strike prices are displayed in columns for each option.
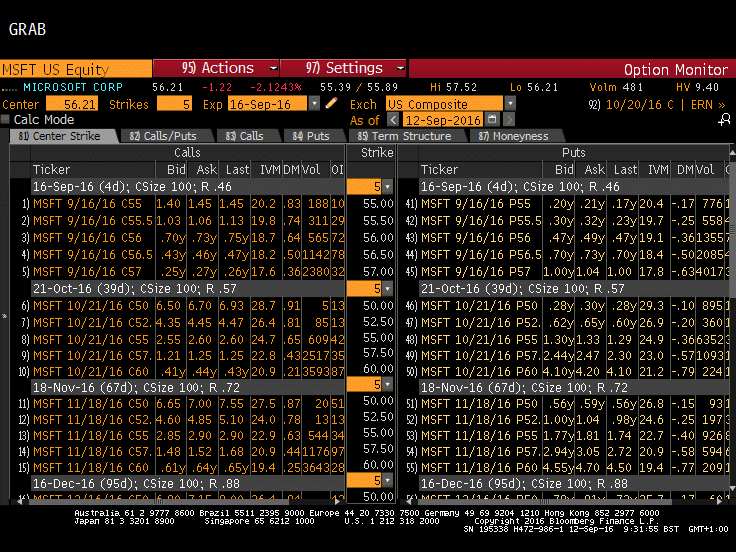
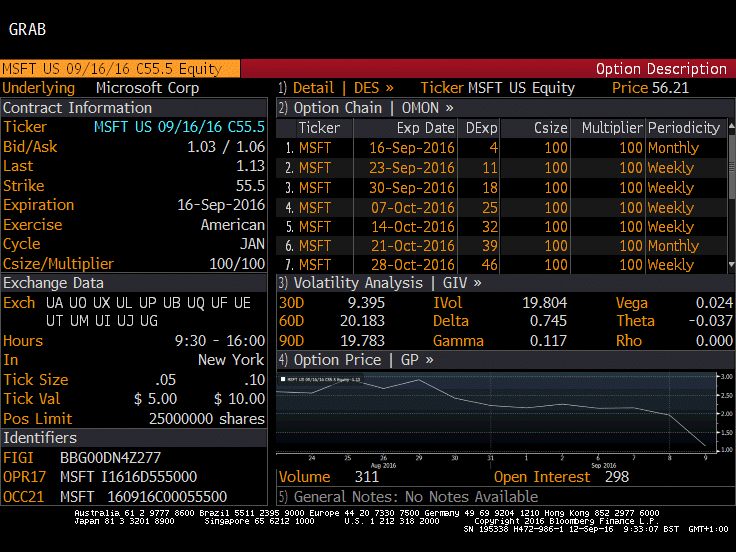
There is an impressive amount of literature about the Greeks available on the Internet. Below you can find list of links which we’ve gathered from our research as the most relevant in terms of quality information about Greeks and Options. Note that the Greeks help traders to read and interpret important measurements of an option’s risk and potential rewards.
Since market conditions are constantly changing, the Greeks provide traders with a means of determining how sensitive a specific trade is to price fluctuations, volatility fluctuations, and the passage of time. Combining an understanding of the Greeks with the powerful insights the risk graphs provide can help you take your options trading to another level.
Further reading on Greeks and Options
- Using “The Greeks” To Understand Options
- Getting to Know the “Greeks”
- Using the “Greeks” to Understand Options
- The Basics of Options Price
- Understanding Option Greeks and Dividends
- Option Greeks
- Meet the Greeks
- Volatility and the Greeks
- Option Greeks – Part 1 (video)
- The Greeks: Delta, Gamma, Theta, Vega, and Rho
- The Greeks – Terry’s Tips





